Note
Go to the end to download the full example code.
Fused Softmax
In this tutorial, you will write a fused softmax operation that is significantly faster than PyTorch’s native op for a particular class of matrices: those whose rows can fit in the GPU’s SRAM.
In doing so, you will learn about:
The benefits of kernel fusion for bandwidth-bound operations.
Reduction operators in Triton.
Motivations
Custom GPU kernels for elementwise additions are educationally valuable but won’t get you very far in practice. Let us consider instead the case of a simple (numerically stabilized) softmax operation:
import torch
import triton
import triton.language as tl
from triton.runtime import driver
DEVICE = triton.runtime.driver.active.get_active_torch_device()
def is_hip():
return triton.runtime.driver.active.get_current_target().backend == "hip"
def is_cdna():
return is_hip() and triton.runtime.driver.active.get_current_target().arch in ('gfx940', 'gfx941', 'gfx942',
'gfx90a', 'gfx908')
def naive_softmax(x):
"""Compute row-wise softmax of X using native pytorch
We subtract the maximum element in order to avoid overflows. Softmax is invariant to
this shift.
"""
# read MN elements ; write M elements
x_max = x.max(dim=1)[0]
# read MN + M elements ; write MN elements
z = x - x_max[:, None]
# read MN elements ; write MN elements
numerator = torch.exp(z)
# read MN elements ; write M elements
denominator = numerator.sum(dim=1)
# read MN + M elements ; write MN elements
ret = numerator / denominator[:, None]
# in total: read 5MN + 2M elements ; wrote 3MN + 2M elements
return ret
When implemented naively in PyTorch, computing y = naive_softmax(x) for \(x \in R^{M \times N}\)
requires reading \(5MN + 2M\) elements from DRAM and writing back \(3MN + 2M\) elements.
This is obviously wasteful; we’d prefer to have a custom “fused” kernel that only reads
X once and does all the necessary computations on-chip.
Doing so would require reading and writing back only \(MN\) bytes, so we could
expect a theoretical speed-up of ~4x (i.e., \((8MN + 4M) / 2MN\)).
The torch.jit.script flags aims to perform this kind of “kernel fusion” automatically
but, as we will see later, it is still far from ideal.
Compute Kernel
Our softmax kernel works as follows: each program loads a set of rows of the input matrix X strided by number of programs, normalizes it and writes back the result to the output Y.
Note that one important limitation of Triton is that each block must have a power-of-two number of elements, so we need to internally “pad” each row and guard the memory operations properly if we want to handle any possible input shapes:
@triton.jit
def softmax_kernel(output_ptr, input_ptr, input_row_stride, output_row_stride, n_rows, n_cols, BLOCK_SIZE: tl.constexpr,
num_stages: tl.constexpr):
# starting row of the program
row_start = tl.program_id(0)
row_step = tl.num_programs(0)
for row_idx in tl.range(row_start, n_rows, row_step, num_stages=num_stages):
# The stride represents how much we need to increase the pointer to advance 1 row
row_start_ptr = input_ptr + row_idx * input_row_stride
# The block size is the next power of two greater than n_cols, so we can fit each
# row in a single block
col_offsets = tl.arange(0, BLOCK_SIZE)
input_ptrs = row_start_ptr + col_offsets
# Load the row into SRAM, using a mask since BLOCK_SIZE may be > than n_cols
mask = col_offsets < n_cols
row = tl.load(input_ptrs, mask=mask, other=-float('inf'))
# Subtract maximum for numerical stability
row_minus_max = row - tl.max(row, axis=0)
# Note that exponentiation in Triton is fast but approximate (i.e., think __expf in CUDA)
numerator = tl.exp(row_minus_max)
denominator = tl.sum(numerator, axis=0)
softmax_output = numerator / denominator
# Write back output to DRAM
output_row_start_ptr = output_ptr + row_idx * output_row_stride
output_ptrs = output_row_start_ptr + col_offsets
tl.store(output_ptrs, softmax_output, mask=mask)
We can create a helper function that enqueues the kernel and its (meta-)arguments for any given input tensor.
properties = driver.active.utils.get_device_properties(DEVICE.index)
NUM_SM = properties["multiprocessor_count"]
NUM_REGS = properties["max_num_regs"]
SIZE_SMEM = properties["max_shared_mem"]
WARP_SIZE = properties["warpSize"]
target = triton.runtime.driver.active.get_current_target()
kernels = {}
def softmax(x):
n_rows, n_cols = x.shape
# The block size of each loop iteration is the smallest power of two greater than the number of columns in `x`
BLOCK_SIZE = triton.next_power_of_2(n_cols)
# Another trick we can use is to ask the compiler to use more threads per row by
# increasing the number of warps (`num_warps`) over which each row is distributed.
# You will see in the next tutorial how to auto-tune this value in a more natural
# way so you don't have to come up with manual heuristics yourself.
num_warps = 8
# Number of software pipelining stages.
num_stages = 4 if SIZE_SMEM > 200000 else 2
# Allocate output
y = torch.empty_like(x)
# pre-compile kernel to get register usage and compute thread occupancy.
kernel = softmax_kernel.warmup(y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE=BLOCK_SIZE,
num_stages=num_stages, num_warps=num_warps, grid=(1, ))
kernel._init_handles()
n_regs = kernel.n_regs
size_smem = kernel.metadata.shared
if is_hip():
# NUM_REGS represents the number of regular purpose registers. On CDNA architectures this is half of all registers available.
# However, this is not always the case. In most cases all registers can be used as regular purpose registers.
# ISA SECTION (3.6.4 for CDNA3)
# VGPRs are allocated out of two pools: regular VGPRs and accumulation VGPRs. Accumulation VGPRs are used
# with matrix VALU instructions, and can also be loaded directly from memory. A wave may have up to 512 total
# VGPRs, 256 of each type. When a wave has fewer than 512 total VGPRs, the number of each type is flexible - it is
# not required to be equal numbers of both types.
NUM_GPRS = NUM_REGS
if is_cdna():
NUM_GPRS = NUM_REGS * 2
# MAX_NUM_THREADS represents maximum number of resident threads per multi-processor.
# When we divide this number with WARP_SIZE we get maximum number of waves that can
# execute on a CU (multi-processor) in parallel.
MAX_NUM_THREADS = properties["max_threads_per_sm"]
max_num_waves = MAX_NUM_THREADS // WARP_SIZE
occupancy = min(NUM_GPRS // WARP_SIZE // n_regs, max_num_waves) // num_warps
else:
occupancy = NUM_REGS // (n_regs * WARP_SIZE * num_warps)
occupancy = min(occupancy, SIZE_SMEM // size_smem)
num_programs = NUM_SM * occupancy
num_programs = min(num_programs, n_rows)
# Create a number of persistent programs.
kernel[(num_programs, 1, 1)](y, x, x.stride(0), y.stride(0), n_rows, n_cols, BLOCK_SIZE, num_stages)
return y
Unit Test
We make sure that we test our kernel on a matrix with an irregular number of rows and columns. This will allow us to verify that our padding mechanism works.
torch.manual_seed(0)
x = torch.randn(1823, 781, device=DEVICE)
y_triton = softmax(x)
y_torch = torch.softmax(x, axis=1)
assert torch.allclose(y_triton, y_torch), (y_triton, y_torch)
As expected, the results are identical.
Benchmark
Here we will benchmark our operation as a function of the number of columns in the input matrix – assuming 4096 rows.
We will then compare its performance against (1) torch.softmax and (2) the naive_softmax defined above.
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'], # argument names to use as an x-axis for the plot
x_vals=[128 * i for i in range(2, 100)], # different possible values for `x_name`
line_arg='provider', # argument name whose value corresponds to a different line in the plot
line_vals=['triton', 'torch', 'naive_softmax'], # possible values for `line_arg``
line_names=["Triton", "Torch", "Naive Softmax"], # label name for the lines
styles=[('blue', '-'), ('green', '-'), ('red', '-')], # line styles
ylabel="GB/s", # label name for the y-axis
plot_name="softmax-performance", # name for the plot. Used also as a file name for saving the plot.
args={'M': 4096}, # values for function arguments not in `x_names` and `y_name`
))
def benchmark(M, N, provider):
x = torch.randn(M, N, device=DEVICE, dtype=torch.float32)
stream = getattr(torch, DEVICE.type).Stream()
getattr(torch, DEVICE.type).set_stream(stream)
if provider == 'torch':
ms = triton.testing.do_bench(lambda: torch.softmax(x, axis=-1))
if provider == 'triton':
ms = triton.testing.do_bench(lambda: softmax(x))
if provider == 'naive_softmax':
ms = triton.testing.do_bench(lambda: naive_softmax(x))
gbps = lambda ms: 2 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3)
return gbps(ms)
benchmark.run(show_plots=True, print_data=True)
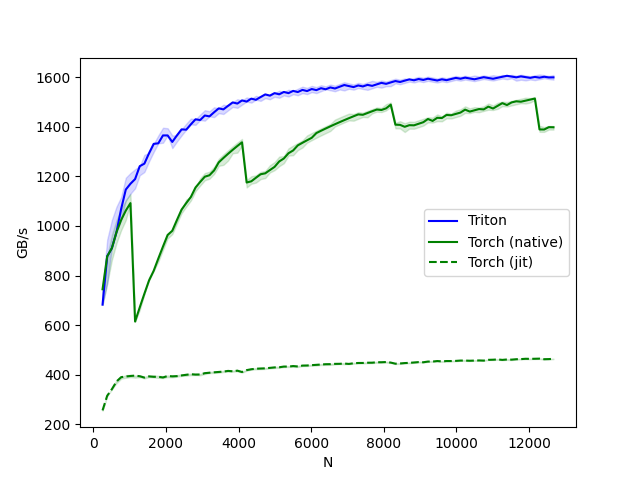
softmax-performance:
N Triton (GB/s) Torch (GB/s) Naive Softmax (GB/s)
0 256.0 513.956690 706.303535 208.257948
1 384.0 708.737943 815.197395 263.187990
2 512.0 844.565311 933.503339 303.632320
3 640.0 846.675898 921.599992 331.369249
4 768.0 906.034985 982.214319 350.416806
5 896.0 976.224147 1026.213342 354.135025
6 1024.0 1028.810820 1076.455430 353.772856
7 1152.0 1021.804279 1065.799258 347.673690
8 1280.0 1070.823276 1111.187055 348.810050
9 1408.0 1114.391493 1139.600028 340.302121
10 1536.0 1144.051343 1164.643071 333.894136
11 1664.0 1188.998755 1183.502693 329.969807
12 1792.0 1209.145827 1202.534467 325.451075
13 1920.0 1232.505586 1227.625994 324.387606
14 2048.0 1249.735200 1244.753335 324.716024
15 2176.0 1262.412203 964.222021 325.835676
16 2304.0 1274.193753 998.892591 325.637137
17 2432.0 1297.707147 1033.938200 326.232602
18 2560.0 1297.571286 1071.408015 327.834273
19 2688.0 1311.572058 1100.912129 329.016589
20 2816.0 1333.561613 1122.348590 328.523600
21 2944.0 1336.056961 1148.634152 331.410065
22 3072.0 1348.361725 1174.824453 333.244812
23 3200.0 1355.294116 1175.560299 335.169302
24 3328.0 1361.993286 1199.789246 336.163758
25 3456.0 1369.244047 1220.730453 337.288562
26 3584.0 1374.607870 1243.264357 337.975243
27 3712.0 1388.633634 1263.098196 339.816113
28 3840.0 1392.589997 1281.157491 340.044817
29 3968.0 1393.153579 1296.891937 340.877615
30 4096.0 1390.235567 1316.683024 338.994426
31 4224.0 1330.827809 1278.095773 342.661132
32 4352.0 1351.763553 1298.569596 345.324861
33 4480.0 1351.427422 1317.270099 346.139227
34 4608.0 1364.413247 1334.880652 347.234276
35 4736.0 1364.331313 1348.081691 348.110976
36 4864.0 1378.909379 1359.290282 349.454693
37 4992.0 1374.518739 1377.202355 350.050250
38 5120.0 1384.141861 1388.705320 350.583294
39 5248.0 1379.979916 1359.296944 351.358999
40 5376.0 1384.782701 1372.948054 351.925183
41 5504.0 1388.152714 1386.648517 353.750655
42 5632.0 1398.706915 1389.137844 352.786147
43 5760.0 1399.198909 1407.399899 355.163131
44 5888.0 1398.044719 1419.815746 354.855434
45 6016.0 1409.556183 1414.581071 356.415395
46 6144.0 1416.954830 1435.003287 357.135148
47 6272.0 1420.882223 1398.765069 357.761141
48 6400.0 1418.967971 1414.489332 358.239977
49 6528.0 1419.344694 1424.809390 359.112023
50 6656.0 1423.400051 1428.057660 359.585913
51 6784.0 1425.760975 1437.315238 360.358041
52 6912.0 1431.552643 1454.890383 360.725641
53 7040.0 1423.941441 1450.962102 361.223193
54 7168.0 1427.671136 1460.494772 361.778104
55 7296.0 1430.846267 1086.541109 362.843134
56 7424.0 1436.508716 1096.839199 363.135491
57 7552.0 1429.586590 1112.059941 363.646031
58 7680.0 1438.668991 1125.434466 363.933538
59 7808.0 1438.828961 1132.460077 364.257880
60 7936.0 1438.256059 1141.131332 364.709526
61 8064.0 1442.637812 1150.397508 365.252941
62 8192.0 1435.085731 1151.073892 363.637947
63 8320.0 1380.106141 1115.917255 361.596207
64 8448.0 1385.361279 1125.668325 362.340958
65 8576.0 1385.203161 1129.118434 363.316778
66 8704.0 1379.315299 1135.071437 364.266894
67 8832.0 1396.316424 1133.716132 365.249680
68 8960.0 1387.637817 1140.209767 366.110104
69 9088.0 1396.560194 1134.714958 366.595524
70 9216.0 1403.042322 1141.751578 367.054183
71 9344.0 1391.670420 1420.815531 367.479196
72 9472.0 1394.633603 1431.080840 368.425915
73 9600.0 1402.401328 1433.637194 369.053339
74 9728.0 1396.321885 1441.599092 370.226187
75 9856.0 1397.299341 1438.572613 369.891957
76 9984.0 1392.227870 1451.246605 370.358251
77 10112.0 1404.357018 1457.374679 371.530828
78 10240.0 1406.624087 1463.571784 371.492391
79 10368.0 1413.607664 1459.960392 369.872909
80 10496.0 1408.136871 1463.582077 370.302041
81 10624.0 1400.468294 1464.710819 370.583934
82 10752.0 1391.592884 1471.394333 371.465793
83 10880.0 1391.825915 1476.068897 372.040890
84 11008.0 1416.856239 1479.296931 372.319414
85 11136.0 1416.854872 1485.635813 372.164773
86 11264.0 1410.603962 1487.646525 372.775292
87 11392.0 1417.487255 1489.182913 373.877905
88 11520.0 1415.663420 1495.609321 373.980085
89 11648.0 1419.864718 1498.737428 374.144541
90 11776.0 1432.426983 1502.374552 374.695348
91 11904.0 1425.557608 1507.850685 374.929133
92 12032.0 1414.027053 1510.852041 375.712663
93 12160.0 1408.951553 1514.236048 375.925925
94 12288.0 1426.596294 1420.388139 376.012274
95 12416.0 1426.730435 1397.345845 374.606182
96 12544.0 1443.305626 1395.348518 375.533730
97 12672.0 1430.092315 1393.376693 375.158879
- In the above plot, we can see that:
Triton is 4x faster than the Torch JIT. This confirms our suspicions that the Torch JIT does not do any fusion here.
Triton is noticeably faster than
torch.softmax– in addition to being easier to read, understand and maintain. Note however that the PyTorch softmax operation is more general and will work on tensors of any shape.
Total running time of the script: (0 minutes 34.832 seconds)