Note
Go to the end to download the full example code.
Layer Normalization¶
In this tutorial, you will write a high-performance layer normalization kernel that runs faster than the PyTorch implementation.
In doing so, you will learn about:
Implementing backward pass in Triton.
Implementing parallel reduction in Triton.
Motivations¶
The LayerNorm operator was first introduced in [BA2016] as a way to improve the performance of sequential models (e.g., Transformers) or neural networks with small batch size. It takes a vector \(x\) as input and produces a vector \(y\) of the same shape as output. The normalization is performed by subtracting the mean and dividing by the standard deviation of \(x\). After the normalization, a learnable linear transformation with weights \(w\) and biases \(b\) is applied. The forward pass can be expressed as follows:
where \(\epsilon\) is a small constant added to the denominator for numerical stability. Let’s first take a look at the forward pass implementation.
import torch
import triton
import triton.language as tl
try:
# This is https://github.com/NVIDIA/apex, NOT the apex on PyPi, so it
# should not be added to extras_require in setup.py.
import apex
HAS_APEX = True
except ModuleNotFoundError:
HAS_APEX = False
DEVICE = triton.runtime.driver.active.get_active_torch_device()
@triton.jit
def _layer_norm_fwd_fused(
X, # pointer to the input
Y, # pointer to the output
W, # pointer to the weights
B, # pointer to the biases
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
eps, # epsilon to avoid division by zero
BLOCK_SIZE: tl.constexpr,
):
# Map the program id to the row of X and Y it should compute.
row = tl.program_id(0)
Y += row * stride
X += row * stride
# Compute mean
mean = 0
_mean = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
a = tl.load(X + cols, mask=cols < N, other=0.).to(tl.float32)
_mean += a
mean = tl.sum(_mean, axis=0) / N
# Compute variance
_var = tl.zeros([BLOCK_SIZE], dtype=tl.float32)
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
x = tl.load(X + cols, mask=cols < N, other=0.).to(tl.float32)
x = tl.where(cols < N, x - mean, 0.)
_var += x * x
var = tl.sum(_var, axis=0) / N
rstd = 1 / tl.sqrt(var + eps)
# Write mean / rstd
tl.store(Mean + row, mean)
tl.store(Rstd + row, rstd)
# Normalize and apply linear transformation
for off in range(0, N, BLOCK_SIZE):
cols = off + tl.arange(0, BLOCK_SIZE)
mask = cols < N
w = tl.load(W + cols, mask=mask)
b = tl.load(B + cols, mask=mask)
x = tl.load(X + cols, mask=mask, other=0.).to(tl.float32)
x_hat = (x - mean) * rstd
y = x_hat * w + b
# Write output
tl.store(Y + cols, y, mask=mask)
Backward pass¶
The backward pass for the layer normalization operator is a bit more involved than the forward pass. Let \(\hat{x}\) be the normalized inputs \(\frac{ x - \text{E}[x] }{ \sqrt{\text{Var}(x) + \epsilon} }\) before the linear transformation, the Vector-Jacobian Products (VJP) \(\nabla_{x}\) of \(x\) are given by:
where \(\odot\) denotes the element-wise multiplication, \(\cdot\) denotes the dot product, and \(\sigma\) is the standard deviation. \(c_1\) and \(c_2\) are intermediate constants that improve the readability of the following implementation.
For the weights \(w\) and biases \(b\), the VJPs \(\nabla_{w}\) and \(\nabla_{b}\) are more straightforward:
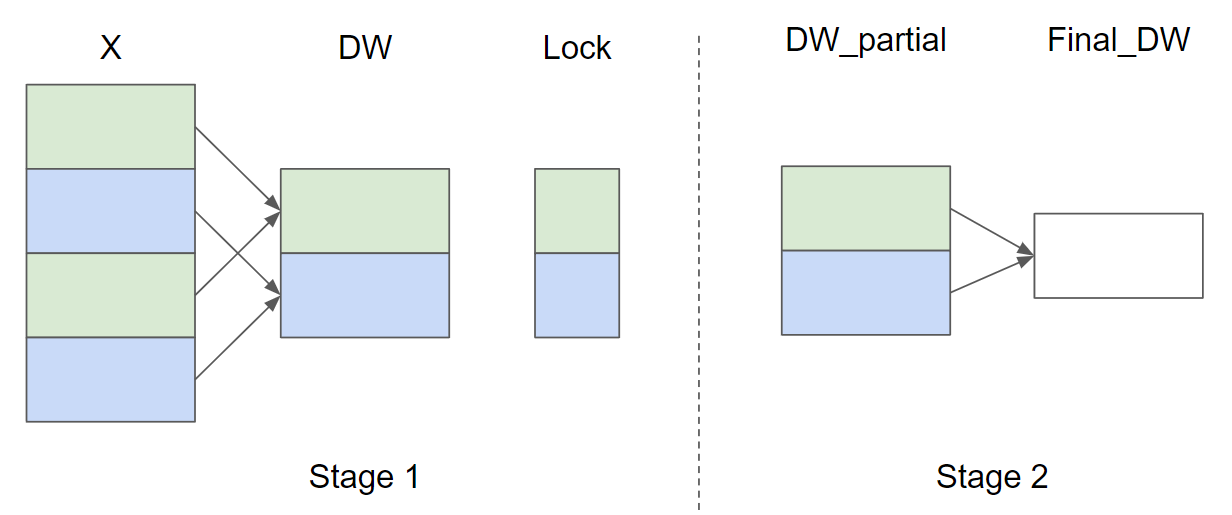
Since the same weights \(w\) and biases \(b\) are used for all rows in the same batch, their gradients need to sum up. To perform this step efficiently, we use a parallel reduction strategy: each kernel instance accumulates partial \(\nabla_{w}\) and \(\nabla_{b}\) across certain rows into one of \(\text{GROUP_SIZE_M}\) independent buffers. These buffers stay in the L2 cache and then are further reduced by another function to compute the actual \(\nabla_{w}\) and \(\nabla_{b}\).
Let the number of input rows \(M = 4\) and \(\text{GROUP_SIZE_M} = 2\), here’s a diagram of the parallel reduction strategy for \(\nabla_{w}\) (\(\nabla_{b}\) is omitted for brevity):
In Stage 1, the rows of X that have the same color share the same buffer and thus a lock is used to ensure that only one kernel instance writes to the buffer at a time.
In Stage 2, the buffers are further reduced to compute the final \(\nabla_{w}\) and \(\nabla_{b}\).
In the following implementation, Stage 1 is implemented by the function _layer_norm_bwd_dx_fused and Stage 2 is implemented by the function _layer_norm_bwd_dwdb.
@triton.jit
def _layer_norm_bwd_dx_fused(DX, # pointer to the input gradient
DY, # pointer to the output gradient
DW, # pointer to the partial sum of weights gradient
DB, # pointer to the partial sum of biases gradient
X, # pointer to the input
W, # pointer to the weights
Mean, # pointer to the mean
Rstd, # pointer to the 1/std
Lock, # pointer to the lock
stride, # how much to increase the pointer when moving by 1 row
N, # number of columns in X
GROUP_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr):
# Map the program id to the elements of X, DX, and DY it should compute.
row = tl.program_id(0)
cols = tl.arange(0, BLOCK_SIZE_N)
mask = cols < N
X += row * stride
DY += row * stride
DX += row * stride
# Offset locks and weights/biases gradient pointer for parallel reduction
lock_id = row % GROUP_SIZE_M
Lock += lock_id
Count = Lock + GROUP_SIZE_M
DW = DW + lock_id * N + cols
DB = DB + lock_id * N + cols
# Load data to SRAM
x = tl.load(X + cols, mask=mask, other=0).to(tl.float32)
dy = tl.load(DY + cols, mask=mask, other=0).to(tl.float32)
w = tl.load(W + cols, mask=mask).to(tl.float32)
mean = tl.load(Mean + row)
rstd = tl.load(Rstd + row)
# Compute dx
xhat = (x - mean) * rstd
wdy = w * dy
xhat = tl.where(mask, xhat, 0.)
wdy = tl.where(mask, wdy, 0.)
c1 = tl.sum(xhat * wdy, axis=0) / N
c2 = tl.sum(wdy, axis=0) / N
dx = (wdy - (xhat * c1 + c2)) * rstd
# Write dx
tl.store(DX + cols, dx, mask=mask)
# Accumulate partial sums for dw/db
partial_dw = (dy * xhat).to(w.dtype)
partial_db = (dy).to(w.dtype)
while tl.atomic_cas(Lock, 0, 1) == 1:
pass
count = tl.load(Count)
# First store doesn't accumulate
if count == 0:
tl.atomic_xchg(Count, 1)
else:
partial_dw += tl.load(DW, mask=mask)
partial_db += tl.load(DB, mask=mask)
tl.store(DW, partial_dw, mask=mask)
tl.store(DB, partial_db, mask=mask)
# need a barrier to ensure all threads finished before
# releasing the lock
tl.debug_barrier()
# Release the lock
tl.atomic_xchg(Lock, 0)
@triton.jit
def _layer_norm_bwd_dwdb(DW, # pointer to the partial sum of weights gradient
DB, # pointer to the partial sum of biases gradient
FINAL_DW, # pointer to the weights gradient
FINAL_DB, # pointer to the biases gradient
M, # GROUP_SIZE_M
N, # number of columns
BLOCK_SIZE_M: tl.constexpr, BLOCK_SIZE_N: tl.constexpr):
# Map the program id to the elements of DW and DB it should compute.
pid = tl.program_id(0)
cols = pid * BLOCK_SIZE_N + tl.arange(0, BLOCK_SIZE_N)
dw = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
db = tl.zeros((BLOCK_SIZE_M, BLOCK_SIZE_N), dtype=tl.float32)
# Iterate through the rows of DW and DB to sum the partial sums.
for i in range(0, M, BLOCK_SIZE_M):
rows = i + tl.arange(0, BLOCK_SIZE_M)
mask = (rows[:, None] < M) & (cols[None, :] < N)
offs = rows[:, None] * N + cols[None, :]
dw += tl.load(DW + offs, mask=mask, other=0.)
db += tl.load(DB + offs, mask=mask, other=0.)
# Write the final sum to the output.
sum_dw = tl.sum(dw, axis=0)
sum_db = tl.sum(db, axis=0)
tl.store(FINAL_DW + cols, sum_dw, mask=cols < N)
tl.store(FINAL_DB + cols, sum_db, mask=cols < N)
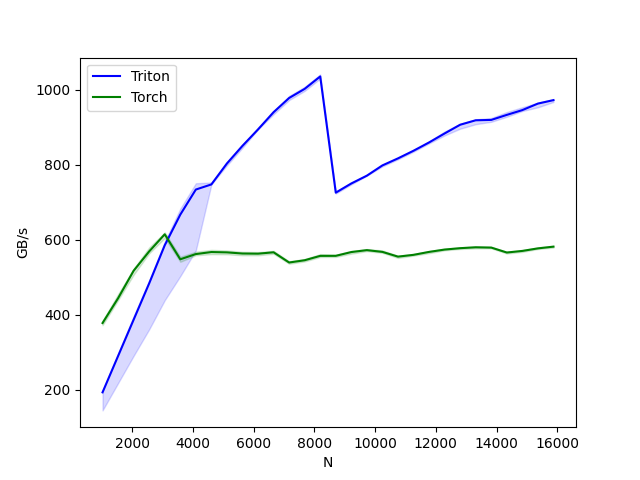
Benchmark¶
We can now compare the performance of our kernel against that of PyTorch.
Here we focus on inputs that have Less than 64KB per feature.
Specifically, one can set 'mode': 'backward' to benchmark the backward pass.
class LayerNorm(torch.autograd.Function):
@staticmethod
def forward(ctx, x, normalized_shape, weight, bias, eps):
# allocate output
y = torch.empty_like(x)
# reshape input data into 2D tensor
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
mean = torch.empty((M, ), dtype=torch.float32, device=x.device)
rstd = torch.empty((M, ), dtype=torch.float32, device=x.device)
# Less than 64KB per feature: enqueue fused kernel
MAX_FUSED_SIZE = 65536 // x.element_size()
BLOCK_SIZE = min(MAX_FUSED_SIZE, triton.next_power_of_2(N))
if N > BLOCK_SIZE:
raise RuntimeError("This layer norm doesn't support feature dim >= 64KB.")
# heuristics for number of warps
num_warps = min(max(BLOCK_SIZE // 256, 1), 8)
# enqueue kernel
_layer_norm_fwd_fused[(M, )]( #
x_arg, y, weight, bias, mean, rstd, #
x_arg.stride(0), N, eps, #
BLOCK_SIZE=BLOCK_SIZE, num_warps=num_warps, num_ctas=1)
ctx.save_for_backward(x, weight, bias, mean, rstd)
ctx.BLOCK_SIZE = BLOCK_SIZE
ctx.num_warps = num_warps
ctx.eps = eps
return y
@staticmethod
def backward(ctx, dy):
x, w, b, m, v = ctx.saved_tensors
# heuristics for amount of parallel reduction stream for DW/DB
N = w.shape[0]
GROUP_SIZE_M = 64
if N <= 8192: GROUP_SIZE_M = 96
if N <= 4096: GROUP_SIZE_M = 128
if N <= 1024: GROUP_SIZE_M = 256
# allocate output
locks = torch.zeros(2 * GROUP_SIZE_M, dtype=torch.int32, device=w.device)
_dw = torch.zeros((GROUP_SIZE_M, N), dtype=x.dtype, device=w.device)
_db = torch.zeros((GROUP_SIZE_M, N), dtype=x.dtype, device=w.device)
dw = torch.empty((N, ), dtype=w.dtype, device=w.device)
db = torch.empty((N, ), dtype=w.dtype, device=w.device)
dx = torch.empty_like(dy)
# enqueue kernel using forward pass heuristics
# also compute partial sums for DW and DB
x_arg = x.reshape(-1, x.shape[-1])
M, N = x_arg.shape
_layer_norm_bwd_dx_fused[(M, )]( #
dx, dy, _dw, _db, x, w, m, v, locks, #
x_arg.stride(0), N, #
BLOCK_SIZE_N=ctx.BLOCK_SIZE, #
GROUP_SIZE_M=GROUP_SIZE_M, #
num_warps=ctx.num_warps)
grid = lambda meta: (triton.cdiv(N, meta['BLOCK_SIZE_N']), )
# accumulate partial sums in separate kernel
_layer_norm_bwd_dwdb[grid](
_dw, _db, dw, db, min(GROUP_SIZE_M, M), N, #
BLOCK_SIZE_M=32, #
BLOCK_SIZE_N=128, num_ctas=1)
return dx, None, dw, db, None
layer_norm = LayerNorm.apply
def test_layer_norm(M, N, dtype, eps=1e-5, device=DEVICE):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device=device)
dy = .1 * torch.randn_like(x)
x.requires_grad_(True)
# forward pass
y_tri = layer_norm(x, w_shape, weight, bias, eps)
y_ref = torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps).to(dtype)
# backward pass (triton)
y_tri.backward(dy, retain_graph=True)
dx_tri, dw_tri, db_tri = [_.grad.clone() for _ in [x, weight, bias]]
x.grad, weight.grad, bias.grad = None, None, None
# backward pass (torch)
y_ref.backward(dy, retain_graph=True)
dx_ref, dw_ref, db_ref = [_.grad.clone() for _ in [x, weight, bias]]
# compare
assert torch.allclose(y_tri, y_ref, atol=1e-2, rtol=0)
assert torch.allclose(dx_tri, dx_ref, atol=1e-2, rtol=0)
assert torch.allclose(db_tri, db_ref, atol=1e-2, rtol=0)
assert torch.allclose(dw_tri, dw_ref, atol=1e-2, rtol=0)
@triton.testing.perf_report(
triton.testing.Benchmark(
x_names=['N'],
x_vals=[512 * i for i in range(2, 32)],
line_arg='provider',
line_vals=['triton', 'torch'] + (['apex'] if HAS_APEX else []),
line_names=['Triton', 'Torch'] + (['Apex'] if HAS_APEX else []),
styles=[('blue', '-'), ('green', '-'), ('orange', '-')],
ylabel='GB/s',
plot_name='layer-norm-backward',
args={'M': 4096, 'dtype': torch.float16, 'mode': 'backward'},
))
def bench_layer_norm(M, N, dtype, provider, mode='backward', eps=1e-5, device=DEVICE):
# create data
x_shape = (M, N)
w_shape = (x_shape[-1], )
weight = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
bias = torch.rand(w_shape, dtype=dtype, device=device, requires_grad=True)
x = -2.3 + 0.5 * torch.randn(x_shape, dtype=dtype, device=device)
dy = .1 * torch.randn_like(x)
x.requires_grad_(True)
quantiles = [0.5, 0.2, 0.8]
def y_fwd():
if provider == "triton":
return layer_norm(x, w_shape, weight, bias, eps) # noqa: F811, E704
if provider == "torch":
return torch.nn.functional.layer_norm(x, w_shape, weight, bias, eps) # noqa: F811, E704
if provider == "apex":
apex_layer_norm = (apex.normalization.FusedLayerNorm(w_shape).to(x.device).to(x.dtype))
return apex_layer_norm(x) # noqa: F811, E704
# forward pass
if mode == 'forward':
gbps = lambda ms: 2 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3)
ms, min_ms, max_ms = triton.testing.do_bench(y_fwd, quantiles=quantiles, rep=500)
# backward pass
if mode == 'backward':
y = y_fwd()
gbps = lambda ms: 3 * x.numel() * x.element_size() * 1e-9 / (ms * 1e-3) # noqa: F811, E704
ms, min_ms, max_ms = triton.testing.do_bench(lambda: y.backward(dy, retain_graph=True), quantiles=quantiles,
grad_to_none=[x], rep=500)
return gbps(ms), gbps(max_ms), gbps(min_ms)
test_layer_norm(1151, 8192, torch.float16)
bench_layer_norm.run(save_path='.', print_data=True)
layer-norm-backward:
N Triton Torch
0 1024.0 122.268655 366.805965
1 1536.0 179.824387 444.144584
2 2048.0 240.941181 511.999982
3 2560.0 307.200008 558.545450
4 3072.0 436.260339 580.535403
5 3584.0 497.202332 512.000004
6 4096.0 581.680452 522.893602
7 4608.0 604.327881 529.148312
8 5120.0 664.216226 541.321594
9 5632.0 711.410503 553.967224
10 6144.0 788.534769 562.809189
11 6656.0 840.757868 572.559140
12 7168.0 915.063803 547.872604
13 7680.0 940.408194 555.180730
14 8192.0 973.306952 561.737163
15 8704.0 691.708608 569.198909
16 9216.0 737.279965 575.999980
17 9728.0 762.980388 579.334969
18 10240.0 787.692335 578.258816
19 10752.0 784.340420 565.894726
20 11264.0 809.389194 571.534892
21 11776.0 853.848973 573.273800
22 12288.0 867.388239 583.984154
23 12800.0 885.302610 585.142878
24 13312.0 875.309554 585.142831
25 13824.0 889.479921 588.255332
26 14336.0 919.957230 576.321603
27 14848.0 952.812845 579.434122
28 15360.0 959.999966 586.073117
29 15872.0 945.230739 587.851864
References¶
Jimmy Lei Ba and Jamie Ryan Kiros and Geoffrey E. Hinton, “Layer Normalization”, Arxiv 2016
Total running time of the script: (0 minutes 29.194 seconds)